Primul meu laborator
Home Cuprins Inapoi Inainte
- 🧔 In acest laborator ne propunem sa masuram perioada de oscilatie (T) a unui pendul gravitational (ex. kendama).
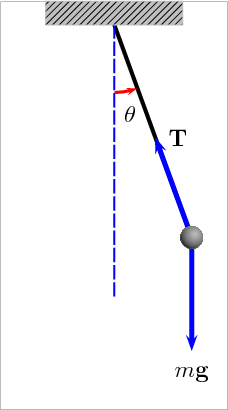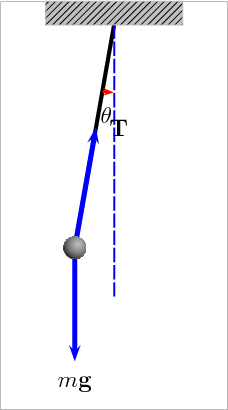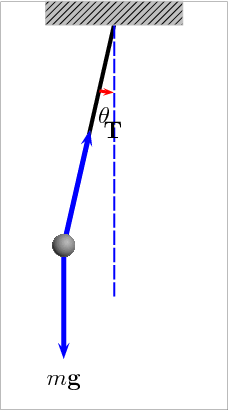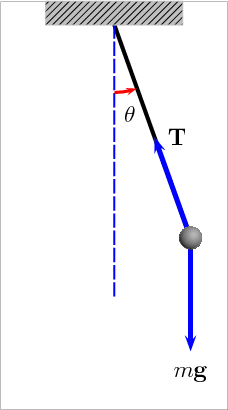
Inregistrarea datelor intr-un tabel
Vom folosi un cronometru pentru a masura durata a 3 oscilatii (in acest fel reducem erorile de masurare).
Vom inregistra datele in tabelul de mai jos:
| Nr. | 3T(s) | T(s) | Tmediu(s) | (T - Tmediu)(s) |
δT(s)
|T - Tmediu| |
δTmediu |
| 1 | 4.2 | 1.4 | 1.384 | 0.016 | 0.016 | 0.0528 |
| 2 | 4.5 | 1.5 | 0.116 | 0.116 | ||
| 3 | 4.15 | 1.38 | -0.004 | 0.004 | ||
| 4 | 3.92 | 1.3 | -0.084 | 0.084 | ||
| 5 | 4.04 | 1.34 | -0.044 | 0.044 |
Calcularea valorii medii si a erorii absolute medii. Scrierea rezultatului masurarii.
T = 3T/3
Valoarea medie: Tmediu = (T1 + T2 + T3 + T4 + T5) : 5 ===> Tmediu = 1.384s
Eroarea de masurare: T - Tmediu
Eroarea absoluta (abaterea absoluta): δT = |T - Tmediu|
Eroarea absoluta medie (abaterea medie): δTmediu = (δT1 + δT2 + δT3 + δT4 + δT5) : 5 ===> δTmediu = 0.0528s
Rezultatul masurat: Tmasurat = Tmediu ± δTmediu ===> T = 1.384 ± 0.0528s
- Mie nu imi este foarte clar... Am inteles ca valoarea adevarata nu poate fi aflata. Totusi, valoarea adevarata ar fi media artitmetica?...
- 🧔 Foarte buna intrebarea! Intr-adevar, media aritmetica nu este valoarea adevarata, dar putem considera ca ea este o valoare apropiata de xA. Sa vedem de ce!
Daca folosim axa numerelor, observam ca media aritmetica a doua numere a si b se afla la mijloc.
De exemplu, in figura de mai jos este reprezentata media aritmetica a numerelor 2 si 8: xM = (2 + 8) : 2 = 5